Subset Sum

Problem Statement

• Example 1

Input: {1, 2, 3, 7}, S=6
Output: True
The given set has a subset whose sum is '6': {1, 2, 3}

• Example 2

Input: {1, 2, 7, 1, 5}, S=10
Output: True
The given set has a subset whose sum is '10': {1, 2, 7}

• Example 3

Input: {1, 3, 4, 8}, S=6
Output: False
The given set does not have any subset whose sum is equal to '6'.

Basic Solution

This problem follows the 0/1 Knapsack pattern and is quite similar to Equal Subset Sum Partition. A basic brute-force solution could be to try all subsets of the given numbers to see if any set has a sum equal to S.

So our brute-force algorithm will look like:

for each number 'i'
    create a new set which INCLUDES number 'i' if it does not exceed 'S', and recursively
        process the remaining numbers
    create a new set WITHOUT number 'i', and recursively process the remaining numbers
return true if any of the above two sets has a sum equal to 'S', otherwise return false

Since this problem is quite similar to Equal Subset Sum Partition, let’s jump directly to the bottom-up dynamic programming solution.

Bottom-up Dynamic Programming

We’ll try to find if we can make all possible sums with every subset to populate the array dp[TotalNumbers][S+1].

For every possible sum s (where 0 <= s <= S), we have two options:

• Exclude the number. In this case, we will see if we can get the sum s from the subset excluding this number => dp[index-1][s]

• Include the number if its value is not more than s. In this case, we will see if we can find a subset to get the remaining sum => dp[index-1][s-num[index]]

If either of the above two scenarios returns true, we can find a subset with a sum equal to s.

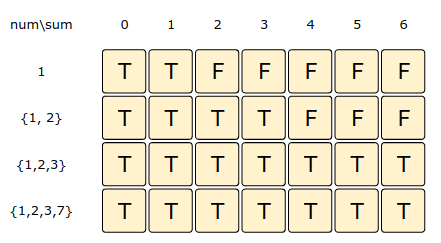
Let’s draw this visually, with the example input {1, 2, 3, 7}, and start with our base case of size zero:

Code

Here is the code for our bottom-up dynamic programming approach:

def can_partition(num, sum):
    n = len(num)
    dp = [[False for x in range(sum+1)] for y in range(n)]

    # populate the sum = 0 columns, as we can always form '0' sum with an empty set
    for i in range(0, n):
        dp[i][0] = True

    # with only one number, we can form a subset only when the required sum is
    # equal to its value
    for s in range(1, sum+1):
        dp[0][s] = True if num[0] == s else False

    # process all subsets for all sums
    for i in range(1, n):
        for s in range(1, sum+1):
            # if we can get the sum 's' without the number at index 'i'
            if dp[i - 1][s]:
                dp[i][s] = dp[i - 1][s]
            elif s >= num[i]:
                # else include the number and see if we can find a subset to get the remaining sum
                dp[i][s] = dp[i - 1][s - num[i]]

    # the bottom-right corner will have our answer.
    return dp[n - 1][sum]


def main():
    print("Can partition: " + str(can_partition([1, 2, 3, 7], 6)))
    print("Can partition: " + str(can_partition([1, 2, 7, 1, 5], 10)))
    print("Can partition: " + str(can_partition([1, 3, 4, 8], 6)))


main()

Challenge

Can we further improve our bottom-up DP solution? Can you find an algorithm that has $O(S)$ space complexity?

def can_partition(num, sum):
    n = len(num)
    dp = [False for x in range(sum+1)]

    # handle sum=0, as we can always have '0' sum with an empty set
    dp[0] = True

    # with only one number, we can have a subset only when the required sum is equal to its value
    for s in range(1, sum+1):
        dp[s] = num[0] == s

    # process all subsets for all sums
    for i in range(1, n):
        for s in range(sum, -1, -1):
            # if dp[s]==true, this means we can get the sum 's' without num[i], hence we can move on to
            # the next number else we can include num[i] and see if we can find a subset to get the
            # remaining sum
            if not dp[s] and s >= num[i]:
                dp[s] = dp[s - num[i]]

    return dp[sum]


def main():
    print("Can partition: " + str(can_partition([1, 2, 3, 7], 6)))
    print("Can partition: " + str(can_partition([1, 2, 7, 1, 5], 10)))
    print("Can partition: " + str(can_partition([1, 3, 4, 8], 6)))


main()

Next