Example 1
Input: {1, 2, 3, 9}
Output: 3
Explanation: We can partition the given set into two subsets where the minimum absolute difference
between the sum of numbers is '3'. Following are the two subsets: {1, 2, 3} & {9}.Example 2
Input: {1, 2, 7, 1, 5}
Output: 0
Explanation: We can partition the given set into two subsets where the minimum absolute difference
between the sum of numbers is '0'. Following are the two subsets: {1, 2, 5} & {7, 1}.Example 3
Input: {1, 3, 100, 4}
Output: 92
Explanation: We can partition the given set into two subsets where the minimum absolute difference
between the sum of numbers is '92'. Here are the two subsets: {1, 3, 4} & {100}.This problem follows the 0/1 Knapsack pattern and can be converted into a Subset Sum problem.
Let’s assume S1 and S2 are the two desired subsets. A basic brute-force solution could be to try adding each element either in S1 or S2, to find the combination that gives the minimum sum difference between the two sets.
So our brute-force algorithm will look like:
for each number 'i'
add number 'i' to S1 and recursively process the remaining numbers
add number 'i' to S2 and recursively process the remaining numbers
return the minimum absolute difference of the above two setsHere is the code for the brute-force solution:
def can_partition(num):
return can_partition_recursive(num, 0, 0, 0)
def can_partition_recursive(num, currentIndex, sum1, sum2):
# base check
if currentIndex == len(num):
return abs(sum1 - sum2)
# recursive call after including the number at the currentIndex in the first set
diff1 = can_partition_recursive(
num, currentIndex + 1, sum1 + num[currentIndex], sum2)
# recursive call after including the number at the currentIndex in the second set
diff2 = can_partition_recursive(
num, currentIndex + 1, sum1, sum2 + num[currentIndex])
return min(diff1, diff2)
def main():
print("Can partition: " + str(can_partition([1, 2, 3, 9])))
print("Can partition: " + str(can_partition([1, 2, 7, 1, 5])))
print("Can partition: " + str(can_partition([1, 3, 100, 4])))
main()We can use memoization to overcome the overlapping sub-problems.
We will be using a two-dimensional array to store the results of the solved sub-problems. We can uniquely identify a sub-problem from currentIndex and Sum1; as Sum2 will always be the sum of the remaining numbers.
Here is the code:
def can_partition(num):
s = sum(num)
dp = [[-1 for x in range(s+1)] for y in range(len(num))]
return can_partition_recursive(dp, num, 0, 0, 0)
def can_partition_recursive(dp, num, currentIndex, sum1, sum2):
# base check
if currentIndex == len(num):
return abs(sum1 - sum2)
# check if we have not already processed similar problem
if dp[currentIndex][sum1] == -1:
# recursive call after including the number at the currentIndex in the first set
diff1 = can_partition_recursive(
dp, num, currentIndex + 1, sum1 + num[currentIndex], sum2)
# recursive call after including the number at the currentIndex in the second set
diff2 = can_partition_recursive(
dp, num, currentIndex + 1, sum1, sum2 + num[currentIndex])
dp[currentIndex][sum1] = min(diff1, diff2)
return dp[currentIndex][sum1]
def main():
print("Can partition: " + str(can_partition([1, 2, 3, 9])))
print("Can partition: " + str(can_partition([1, 2, 7, 1, 5])))
print("Can partition: " + str(can_partition([1, 3, 100, 4])))
main()Let’s assume S represents the total sum of all the numbers. So what we are trying to achieve in this problem is to find a subset whose sum is as close to S/2 as possible, because if we can partition the given set into two subsets of an equal sum, we get the minimum difference i.e. zero. This transforms our problem to Subset Sum, where we try to find a subset whose sum is equal to a given number– S/2 in our case. If we can’t find such a subset, then we will take the subset which has the sum closest to S/2. This is easily possible, as we will be calculating all possible sums with every subset.
Essentially, we need to calculate all the possible sums up to S/2 for all numbers. So how do we populate the array dp[TotalNumbers][S/2+1] in the bottom-up fashion?
For every possible sum s (where 0 <= s <= S/2), we have two options:
Exclude the number. In this case, we will see if we can get the sum s from the subset excluding this number => dp[index-1][s]
Include the number if its value is not more than s. In this case, we will see if we can find a subset to get the remaining sum => dp[index-1][s-num[index]]
If either of the two above scenarios is true, we can find a subset with a sum equal to s. We should dig into this before we can learn how to find the closest subset.
Let’s draw this visually, with the example input {1, 2, 3, 9}. Since the total sum is 15, therefore, we will try to find a subset whose sum is equal to the half of it i.e. 7.
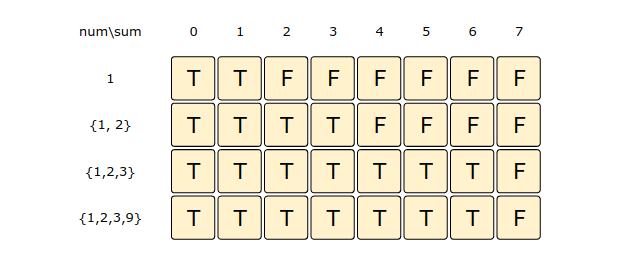
7. So what is the closest subset we can find? We can find such a subset if we start moving backward in the last row from the bottom right corner to find the first T. The first T in the above diagram is the sum 6, which means we can find a subset whose sum is equal to 6. This means the other set will have a sum of 9, and the minimum difference will be 3.Here is the code for our bottom-up dynamic programming approach:
def can_partition(num):
s = sum(num)
n = len(num)
dp = [[False for x in range(int(s/2)+1)] for y in range(n)]
# populate the s=0 columns, as we can always form '0' sum with an empty set
for i in range(0, n):
dp[i][0] = True
# with only one number, we can form a subset only when the required sum is equal to that number
for j in range(1, int(s/2)+1):
dp[0][j] = num[0] == j
# process all subsets for all sums
for i in range(1, n):
for j in range(1, int(s/2)+1):
# if we can get the sum 's' without the number at index 'i'
if dp[i - 1][j]:
dp[i][j] = dp[i - 1][j]
elif j >= num[i]:
# else include the number and see if we can find a subset to get the remaining sum
dp[i][j] = dp[i - 1][j - num[i]]
sum1 = 0
# find the largest index in the last row which is true
for i in range(int(s/2), -1, -1):
if dp[n - 1][i]:
sum1 = i
break
sum2 = s - sum1
return abs(sum2 - sum1)
def main():
print("Can partition: " + str(can_partition([1, 2, 3, 9])))
print("Can partition: " + str(can_partition([1, 2, 7, 1, 5])))
print("Can partition: " + str(can_partition([1, 3, 100, 4])))
main()N represents total numbers and S is the total sum of all the numbers.✓→ Count of Subset Sum