Count of Subset Sum

Problem Statement

• Example 1

Input: {1, 2, 3, 4}
Output: True
Explanation: The given set can be partitioned into two subsets with equal sum: {1, 4} & {2, 3}

• Example 2

Input: {1, 1, 3, 4, 7}
Output: True
Explanation: The given set can be partitioned into two subsets with equal sum: {1, 3, 4} & {1, 7}

• Example 3

Input: {2, 3, 4, 6}
Output: False
Explanation: The given set cannot be partitioned into two subsets with equal sum.

Basic Solution

This problem follows the 0/1 Knapsack pattern. A basic brute-force solution could be to try all combinations of partitioning the given numbers into two sets to see if any pair of sets has an equal sum.

Assume if S represents the total sum of all the given numbers, then the two equal subsets must have a sum equal to S/2. This essentially transforms our problem to: "Find a subset of the given numbers that has a total sum of S/2".

So our brute-force algorithm will look like:

for each number 'i' 
    create a new set which INCLUDES number 'i' if it does not exceed 'S/2', and recursively 
        process the remaining numbers
    create a new set WITHOUT number 'i', and recursively process the remaining items 
return true if any of the above sets has a sum equal to 'S/2', otherwise return false

Code

Here is the code for the brute-force solution:

def can_partition(num):
    s = sum(num)
    # if 's' is a an odd number, we can't have two subsets with equal sum
    if s % 2 != 0:
        return False

    return can_partition_recursive(num, s / 2, 0)


def can_partition_recursive(num, sum, currentIndex):
    # base check
    if sum == 0:
        return True

    n = len(num)
    if n == 0 or currentIndex >= n:
        return False

    # recursive call after choosing the number at the `currentIndex`
    # if the number at `currentIndex` exceeds the sum, we shouldn't process this
    if num[currentIndex] <= sum:
        if(can_partition_recursive(num, sum - num[currentIndex], currentIndex + 1)):
            return True

    # recursive call after excluding the number at the 'currentIndex'
    return can_partition_recursive(num, sum, currentIndex + 1)


def main():
    print("Can partition: " + str(can_partition([1, 2, 3, 4])))
    print("Can partition: " + str(can_partition([1, 1, 3, 4, 7])))
    print("Can partition: " + str(can_partition([2, 3, 4, 6])))


main()

Top-down Dynamic Programming with Memoization

We can use memoization to overcome the overlapping sub-problems. As stated in previous lessons, memoization is when we store the results of all the previously solved sub-problems return the results from memory if we encounter a problem that has already been solved.

Since we need to store the results for every subset and for every possible sum, therefore we will be using a two-dimensional array to store the results of the solved sub-problems. The first dimension of the array will represent different subsets and the second dimension will represent different ‘sums’ that we can calculate from each subset. These two dimensions of the array can also be inferred from the two changing values (sum and currentIndex) in our recursive function canPartitionRecursive().

Code

Here is the code for Top-down DP with memoization:

def can_partition(num):
    s = sum(num)

    # if 's' is a an odd number, we can't have two subsets with equal sum
    if s % 2 != 0:
        return False

    # initialize the 'dp' array, -1 for default, 1 for true and 0 for false
    dp = [[-1 for x in range(int(s/2)+1)] for y in range(len(num))]
    return True if can_partition_recursive(dp, num, int(s / 2), 0) == 1 else False


def can_partition_recursive(dp, num, sum, currentIndex):
    # base check
    if sum == 0:
        return 1

    n = len(num)
    if n == 0 or currentIndex >= n:
        return 0

    # if we have not already processed a similar problem
    if dp[currentIndex][sum] == -1:
        # recursive call after choosing the number at the currentIndex
        # if the number at currentIndex exceeds the sum, we shouldn't process this
        if num[currentIndex] <= sum:
            if can_partition_recursive(dp, num, sum - num[currentIndex], currentIndex + 1) == 1:
                dp[currentIndex][sum] = 1
                return 1

        # recursive call after excluding the number at the currentIndex
        dp[currentIndex][sum] = can_partition_recursive(
            dp, num, sum, currentIndex + 1)

    return dp[currentIndex][sum]


def main():
    print("Can partition: " + str(can_partition([1, 2, 3, 4])))
    print("Can partition: " + str(can_partition([1, 1, 3, 4, 7])))
    print("Can partition: " + str(can_partition([2, 3, 4, 6])))


main()

Bottom-up Dynamic Programming

Let’s try to populate our dp[][] array from the above solution, working in a bottom-up fashion. Essentially, we want to find if we can make all possible sums with every subset. This means, dp[i][s] will be ‘true’ if we can make sum s from the first i numbers.

So, for each number at index i (0 <= i < num.length) and sum s (0 <= s <= S/2), we have two options:

Exclude the number. In this case, we will see if we can get s from the subset excluding this number: dp[i-1][s] Include the number if its value is not more than s. In this case, we will see if we can find a subset to get the remaining sum: dp[i-1][s-num[i]] If either of the two above scenarios is true, we can find a subset of numbers with a sum equal to s.

Let’s start with our base case of zero capacity:

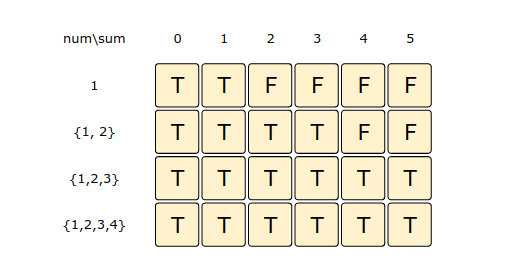
From the above visualization, we can clearly see that it is possible to partition the given set into two subsets with equal sums, as shown by bottom-right cell: dp[3][5] => T.

Code

Here is the code for our bottom-up dynamic programming approach:

def can_partition(num):
    s = sum(num)

    # if 's' is a an odd number, we can't have two subsets with same total
    if s % 2 != 0:
        return False

    # we are trying to find a subset of given numbers that has a total sum of 's/2'.
    s = int(s / 2)

    n = len(num)
    dp = [[False for x in range(s+1)] for y in range(n)]

    # populate the sum=0 column, as we can always have '0' sum without including
    # any element
    for i in range(0, n):
        dp[i][0] = True

    # with only one number, we can form a subset only when the required sum is
    # equal to its value
    for j in range(1, s+1):
        dp[0][j] = num[0] == j

    # process all subsets for all sums
    for i in range(1, n):
        for j in range(1, s+1):
            # if we can get the sum 'j' without the number at index 'i'
            if dp[i - 1][j]:
                dp[i][j] = dp[i - 1][j]
            elif j >= num[i]:  # else if we can find a subset to get the remaining sum
                dp[i][j] = dp[i - 1][j - num[i]]

    # the bottom-right corner will have our answer.
    return dp[n - 1][s]


def main():
    print("Can partition: " + str(can_partition([1, 2, 3, 4])))
    print("Can partition: " + str(can_partition([1, 1, 3, 4, 7])))
    print("Can partition: " + str(can_partition([2, 3, 4, 6])))


main()

Next