Rod Cutting

Problem Statement

• Example

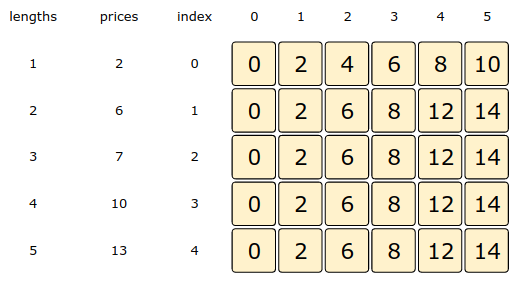
Lengths: [1, 2, 3, 4, 5]
Prices: [2, 6, 7, 10, 13]
Rod Length: 5

Let’s try different combinations of cutting the rod:

Five pieces of length 1 => 10 price
Two pieces of length 2 and one piece of length 1 => 14 price
One piece of length 3 and two pieces of length 1 => 11 price
One piece of length 3 and one piece of length 2 => 13 price
One piece of length 4 and one piece of length 1 => 12 price
One piece of length 5 => 13 price

Basic Solution

This problem can be mapped to the Unbounded Knapsack pattern. The Weights array of the Unbounded Knapsack problem is equivalent to the Lengths array, and Profits is equivalent to Prices.

A basic brute-force solution could be to try all combinations of the given rod lengths to choose the one with the maximum sale price. This is what our algorithm will look like:

for each rod length 'i' 
    create a new set which includes one quantity of length 'i', and recursively process 
        all rod lengths for the remaining length 
    create a new set without rod length 'i', and recursively process for remaining rod lengths
return the set from the above two sets with a higher sales price

Since this problem is quite similar to Unbounded Knapsack , let’s jump directly to the bottom-up dynamic solution.

Bottom-up Dynamic Programming

Let’s try to populate our dp[][] array in a bottom-up fashion. Essentially, what we want to achieve is: “Find the maximum sales price for every rod length and for every possible sales price”.

So for every possible rod length len (0<= len <= n), we have two options:

• Exclude the piece. In this case, we will take whatever price we get from the rod length excluding this piece => dp[index-1][len]

• Include the piece if its length is not more than ‘len’. In this case, we include its price plus whatever price we get from the remaining rod length => prices[index] + dp[index][len-lengths[index]]

Finally, we have to take the maximum of the above two values:

dp[index][len] = max (dp[index-1][len], prices[index] + dp[index][len-lengths[index]])

Let’s draw this visually, with the example:

Lengths: [1, 2, 3, 4, 5]  
Prices: [2, 6, 7, 10, 13]  
Rod Length: 5

Let’s start with our base case of zero size:

Code

Here is the code for our bottom-up dynamic programming approach:

def solve_rod_cutting(lengths, prices, n):
    lengthCount = len(lengths)
    # base checks
    if n <= 0 or lengthCount == 0 or len(prices) != lengthCount:
        return 0

    dp = [[0 for _ in range(n+1)] for _ in range(lengthCount)]

    # process all rod lengths for all prices
    for i in range(lengthCount):
        for length in range(1, n+1):
            p1, p2 = 0, 0
            if lengths[i] <= length:
                p1 = prices[i] + dp[i][length - lengths[i]]
            if i > 0:
                p2 = dp[i - 1][length]
            dp[i][length] = max(p1, p2)

    # maximum price will be at the bottom-right corner.
    return dp[lengthCount - 1][n]


def main():
    print(solve_rod_cutting([1, 2, 3, 4, 5], [2, 6, 7, 10, 13], 5))


main()

Find the selected items

As we know, the final price is at the right-bottom corner; hence we will start from there to find the rod lengths.

As you remember, at every step we had two options: include a rod piece or skip it. If we skip it, then we take the price from the cell right above it; if we include it, then we jump to the remaining length to find more pieces.

Let' s understand this from the above example:

• 14 did come from the top cell, so we jump to the fourth row.

• 14 came from the top cell, so we jump to the third row.

• Again, 14 came from the top cell, so we jump to the second row.

• Now 14 is different from the top cell, so we must include rod of length 2. After this, we subtract the price of the rod of length 2 from 14 and jump to that cell.

• 8 is different than the top cell, so we must include rod of length 2 again. After this, we subtract the price of the rod of length 2 from 8 and jump to that cell.

• 2 did come from the top cell, so we jump to the first row.

• Now we must include a piece of length 1. So the desired rod lengths are {2, 2, 1}.

Next