Coin Change

Introduction

• Example

Denominations: {1,2,3}
Total amount: 5
Output: 5
Explanation: There are five ways to make the change for '5', here are those ways:
  1. {1,1,1,1,1} 
  2. {1,1,1,2} 
  3. {1,2,2}
  4. {1,1,3}
  5. {2,3}

Problem Statement

Basic Solution

A basic brute-force solution could be to try all combinations of the given coins to select the ones that give a total sum of T. This is what our algorithm will look like:

for each coin 'c' 
    create a new set which includes one quantity of coin 'c' if it does not exceed 'T', and 
        recursively call to process all coins 
    create a new set without coin 'c', and recursively call to process the remaining coins 
return the count of sets who have a sum equal to 'T'

This problem is quite similar to Count of Subset Sum. The only difference here is that after including the item (i.e., coin), we recursively call to process all the items (including the current coin). In Count of Subset Sum, however, we were recursively calling to process only the remaining items.

Code

Here is the code for the brute-force solution:

def count_change(denominations, total):
    return count_change_recursive(denominations, total, 0)


def count_change_recursive(denominations, total, currentIndex):
    # base checks
    if total == 0:
        return 1

    n = len(denominations)
    if n == 0 or currentIndex >= n:
        return 0

    # recursive call after selecting the coin at the currentIndex
    # if the coin at currentIndex exceeds the total, we shouldn't process this
    sum1 = 0
    if denominations[currentIndex] <= total:
        sum1 = count_change_recursive(
            denominations, total - denominations[currentIndex], currentIndex)

    # recursive call after excluding the coin at the currentIndex
    sum2 = count_change_recursive(denominations, total, currentIndex + 1)

    return sum1 + sum2


def main():
    print(count_change([1, 2, 3], 5))


main()

Let’s try to find a better solution.

Top-down Dynamic Programming with Memoization

We can use memoization to overcome the overlapping sub-problems. We will be using a two-dimensional array to store the results of solved sub-problems. As mentioned above, we need to store results for every coin combination and for every possible sum:

Code

Here is the code for Top-down DP with memoization:

def count_change(denominations, total):
    dp = [[-1 for _ in range(total+1)] for _ in range(len(denominations))]
    return count_change_recursive(dp, denominations, total, 0)


def count_change_recursive(dp, denominations, total, currentIndex):
    # base checks
    if total == 0:
        return 1

    n = len(denominations)
    if n == 0 or currentIndex >= n:
        return 0

    if dp[currentIndex][total] != -1:
        return dp[currentIndex][total]

    # recursive call after selecting the coin at the currentIndex
    # if the coin at currentIndex exceeds the total, we shouldn't process this
    sum1 = 0
    if denominations[currentIndex] <= total:
        sum1 = count_change_recursive(
            dp, denominations, total - denominations[currentIndex], currentIndex)

    # recursive call after excluding the coin at the currentIndex
    sum2 = count_change_recursive(dp, denominations, total, currentIndex + 1)

    dp[currentIndex][total] = sum1 + sum2
    return dp[currentIndex][total]


def main():
    print(count_change([1, 2, 3], 5))


main()

Bottom-up Dynamic Programming

We will try to find if we can make all possible sums, with every combination of coins, to populate the array dp[TotalDenominations][Total+1].

So for every possible total t (0<= t <= Total) and for every possible coin index (0 <= index < denominations.length), we have two options:

• Exclude the coin. Count all the coin combinations without the given coin up to the total t => dp[index-1][t]

• Include the coin if its value is not more than t. In this case, we will count all the coin combinations to get the remaining total: dp[index][t-denominations[index]]

Finally, to find the total combinations, we will add both the above two values:

dp[index][t] = dp[index-1][t] + dp[index][t-denominations[index]]

Let’s draw this visually with the following example:

Denominations: [1, 2, 3]  
Total: 5

Let’s start with our base case of zero total:

Code

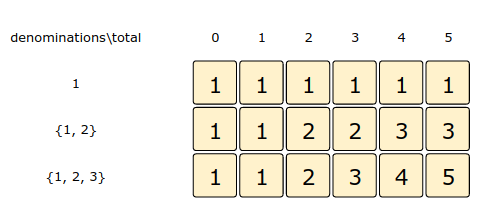
Here is the code for our bottom-up dynamic programming approach:

def count_change(denominations, total):
    n = len(denominations)
    dp = [[0 for _ in range(total+1)] for _ in range(n)]

    # populate the total = 0 columns, as we will always have an empty set for zero total
    for i in range(n):
        dp[i][0] = 1

    # process all sub-arrays for all capacities
    for i in range(n):
        for t in range(1, total+1):
            if i > 0:
                dp[i][t] = dp[i - 1][t]
            if t >= denominations[i]:
                dp[i][t] += dp[i][t - denominations[i]]

    # total combinations will be at the bottom-right corner.
    return dp[n - 1][total]


def main():
    print(count_change([1, 2, 3], 5))


main()

Next