Minimum Coin Change

Introduction

• Example 1

Denominations: {1,2,3}
Total amount: 5
Output: 2
Explanation: We need a minimum of two coins {2,3} to make a total of '5'

• Example 2

Denominations: {1,2,3}
Total amount: 11
Output: 4
Explanation: We need a minimum of four coins {2,3,3,3} to make a total of '11'

Problem Statement

Basic Solution

A basic brute-force solution could be to try all combinations of the given coins to select the ones that give a total sum of T. This is what our algorithm will look like:

for each coin 'c' 
    create a new set which includes one quantity of coin 'c' if it does not exceed 'T', and 
        recursively call to process all coins 
    create a new set without coin 'c', and recursively call to process the remaining coins 
return the count of coins from the above two sets with a smaller number of coins

Code

Here is the code for the brute-force solution:

import math


def count_change(denominations, total):
    result = count_change_recursive(denominations, total, 0)
    return -1 if result == math.inf else result


def count_change_recursive(denominations, total, currentIndex):
    # base check
    if total == 0:
        return 0

    n = len(denominations)
    if n == 0 or currentIndex >= n:
        return math.inf

    # recursive call after selecting the coin at the currentIndex
    # if the coin at currentIndex exceeds the total, we shouldn't process this
    count1 = math.inf
    if denominations[currentIndex] <= total:
        res = count_change_recursive(
            denominations, total - denominations[currentIndex], currentIndex)
        if res != math.inf:
            count1 = res + 1

    # recursive call after excluding the coin at the currentIndex
    count2 = count_change_recursive(denominations, total, currentIndex + 1)

    return min(count1, count2)


def main():
    print(count_change([1, 2, 3], 5))
    print(count_change([1, 2, 3], 11))
    print(count_change([1, 2, 3], 7))
    print(count_change([3, 5], 7))


main()

Let’s try to find a better solution.

Top-down Dynamic Programming with Memoization

We can use memoization to overcome the overlapping sub-problems. We will be using a two-dimensional array to store the results of solved sub-problems. As mentioned above, we need to store results for every coin combination and for every possible sum:

Code

Here is the code:

import math


def count_change(denominations, total):
    dp = [[-1 for _ in range(total+1)] for _ in range(len(denominations))]
    result = count_change_recursive(dp, denominations, total, 0)
    return -1 if result == math.inf else result


def count_change_recursive(dp, denominations, total, currentIndex):
    # base check
    if total == 0:
        return 0
    n = len(denominations)
    if n == 0 or currentIndex >= n:
        return math.inf

    # check if we have not already processed a similar sub-problem
    if dp[currentIndex][total] == -1:
        # recursive call after selecting the coin at the currentIndex
        # if the coin at currentIndex exceeds the total, we shouldn't process this
        count1 = math.inf
        if denominations[currentIndex] <= total:
            res = count_change_recursive(
                dp, denominations, total - denominations[currentIndex], currentIndex)
            if res != math.inf:
                count1 = res + 1

        # recursive call after excluding the coin at the currentIndex
        count2 = count_change_recursive(
            dp, denominations, total, currentIndex + 1)
        dp[currentIndex][total] = min(count1, count2)

    return dp[currentIndex][total]


def main():
    print(count_change([1, 2, 3], 5))
    print(count_change([1, 2, 3], 11))
    print(count_change([1, 2, 3], 7))
    print(count_change([3, 5], 7))


main()

Bottom-up Dynamic Programming

Let’s try to populate our array dp[TotalDenominations][Total+1] for every possible total with a minimum number of coins needed.

So for every possible total t (0<= t <= Total) and for every possible coin index (0 <= index < denominations.length), we have two options:

• Exclude the coin: In this case, we will take the minimum coin count from the previous set => dp[index-1][t]

• Include the coin if its value is not more than t: In this case, we will take the minimum count needed to get the remaining total, plus include 1 for the current coin => dp[index][t-denominations[index]] + 1

Finally, we will take the minimum of the above two values for our solution:

dp[index][t] = min(dp[index-1][t], dp[index][t-denominations[index]] + 1)

Let’s draw this visually with the following example:

Denominations: [1, 2, 3]  
Total: 7

Let’s start with our base case of zero total:

Code

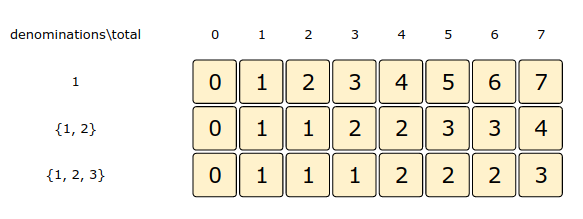
Here is the code for our bottom-up dynamic programming approach:

import math


def count_change(denominations, total):
    n = len(denominations)
    dp = [[math.inf for _ in range(total+1)] for _ in range(n)]

    # populate the total=0 columns, as we don't need any coin to make zero total
    for i in range(n):
        dp[i][0] = 0

    for i in range(n):
        for t in range(1, total+1):
            if i > 0:
                dp[i][t] = dp[i - 1][t]  # exclude the coin
            if t >= denominations[i]:
                if dp[i][t - denominations[i]] != math.inf:
                    # include the coin
                    dp[i][t] = min(dp[i][t], dp[i][t - denominations[i]] + 1)

    # total combinations will be at the bottom-right corner.
    return -1 if dp[n - 1][total] == math.inf else dp[n - 1][total]


def main():
    print(count_change([1, 2, 3], 5))
    print(count_change([1, 2, 3], 11))
    print(count_change([1, 2, 3], 7))
    print(count_change([3, 5], 7))


main()

Next