Given the weights and profits of N items, we are asked to put these items in a knapsack that has a capacity C. The goal is to get the maximum profit from the items in the knapsack. The only difference between the 0/1 Knapsack problem and this problem is that we are allowed to use an unlimited quantity of an item.
Let’s take the example of Merry, who wants to carry some fruits in the knapsack to get maximum profit. Here are the weights and profits of the fruits:
Items: { Apple, Orange, Melon }
Weights: { 1, 2, 3 }
Profits: { 15, 20, 50 }
Knapsack capacity: 5
Let’s try to put different combinations of fruits in the knapsack, such that their total weight is not more than 5.
5 Apples (total weight 5) => 75 profit
1 Apple + 2 Oranges (total weight 5) => 55 profit
2 Apples + 1 Melon (total weight 5) => 80 profit
1 Orange + 1 Melon (total weight 5) => 70 profit
This shows that 2 apples + 1 melon is the best combination, as it gives us the maximum profit and the total weight does not exceed the capacity.
Given two integer arrays to represent weights and profits of N items, we need to find a subset of these items which will give us maximum profit such that their cumulative weight is not more than a given number C. We can assume an infinite supply of item quantities; therefore, each item can be selected multiple times.
A basic brute-force solution could be to try all combinations of the given items to choose the one with maximum profit and a weight that doesn’t exceed C. This is what our algorithm will look like:
for each item 'i'
create a new set which includes one quantity of item 'i' if it does not exceed the capacity, and
recursively call to process all items
create a new set without item 'i', and recursively process the remaining items
return the set from the above two sets with higher profitThe only difference between the 0/1 Knapsack problem and this one is that, after including the item, we recursively call to process all the items (including the current item). In 0/1 Knapsack, however, we recursively call to process the remaining items.
Here is the code for the brute-force solution:
def solve_knapsack(profits, weights, capacity):
return solve_knapsack_recursive(profits, weights, capacity, 0)
def solve_knapsack_recursive(profits, weights, capacity, currentIndex):
n = len(profits)
# base checks
if capacity <= 0 or n == 0 or len(weights) != n or currentIndex >= n:
return 0
# recursive call after choosing the items at the currentIndex, note that we recursive call on all
# items as we did not increment currentIndex
profit1 = 0
if weights[currentIndex] <= capacity:
profit1 = profits[currentIndex] + solve_knapsack_recursive(
profits, weights, capacity - weights[currentIndex], currentIndex)
# recursive call after excluding the element at the currentIndex
profit2 = solve_knapsack_recursive(
profits, weights, capacity, currentIndex + 1)
return max(profit1, profit2)
def main():
print(solve_knapsack([15, 50, 60, 90], [1, 3, 4, 5], 8))
print(solve_knapsack([15, 50, 60, 90], [1, 3, 4, 5], 6))
main()The time complexity of the above algorithm is exponential , where represents the total number of items. The space complexity will be to store the recursion stack.
Let’s try to find a better solution.
Once again, we can use memoization to overcome the overlapping sub-problems.
We will be using a two-dimensional array to store the results of solved sub-problems. As mentioned above, we need to store results for every sub-array and for every possible capacity. Here is the code:
def solve_knapsack(profits, weights, capacity):
dp = [[-1 for _ in range(capacity+1)] for _ in range(len(profits))]
return solve_knapsack_recursive(dp, profits, weights, capacity, 0)
def solve_knapsack_recursive(dp, profits, weights, capacity, currentIndex):
n = len(profits)
# base checks
if capacity <= 0 or n == 0 or len(weights) != n or currentIndex >= n:
return 0
# check if we have not already processed a similar sub-problem
if dp[currentIndex][capacity] == -1:
# recursive call after choosing the items at the currentIndex, note that we
# recursive call on all items as we did not increment currentIndex
profit1 = 0
if weights[currentIndex] <= capacity:
profit1 = profits[currentIndex] + solve_knapsack_recursive(
dp, profits, weights, capacity - weights[currentIndex], currentIndex)
# recursive call after excluding the element at the currentIndex
profit2 = solve_knapsack_recursive(
dp, profits, weights, capacity, currentIndex + 1)
dp[currentIndex][capacity] = max(profit1, profit2)
return dp[currentIndex][capacity]
def main():
print(solve_knapsack([15, 50, 60, 90], [1, 3, 4, 5], 8))
print(solve_knapsack([15, 50, 60, 90], [1, 3, 4, 5], 6))
main()What is the time and space complexity of the above solution? Since our memoization array dp[profits.length][capacity+1] stores the results for all the subproblems, we can conclude that we will not have more than subproblems (where ‘N’ is the number of items and C is the knapsack capacity). This means that our time complexity will be .
The above algorithm will be using space for the memoization array. Other than that, we will use space for the recursion call-stack. So the total space complexity will be , which is asymptotically equivalent to .
Let’s try to populate our dp[][] array from the above solution, working in a bottom-up fashion. Essentially, what we want to achieve is: “Find the maximum profit for every sub-array and for every possible capacity”.
So for every possible capacity c (0 <= c <= capacity), we have two options:
Exclude the item. In this case, we will take whatever profit we get from the sub-array excluding this item: dp[index-1][c]
Include the item if its weight is not more than the c. In this case, we include its profit plus whatever profit we get from the remaining capacity: profit[index] + dp[index][c-weight[index]]
Finally, we have to take the maximum of the above two values:
dp[index][c] = max (dp[index-1][c], profit[index] + dp[index][c-weight[index]])Let’s start with our base case of zero capacity:
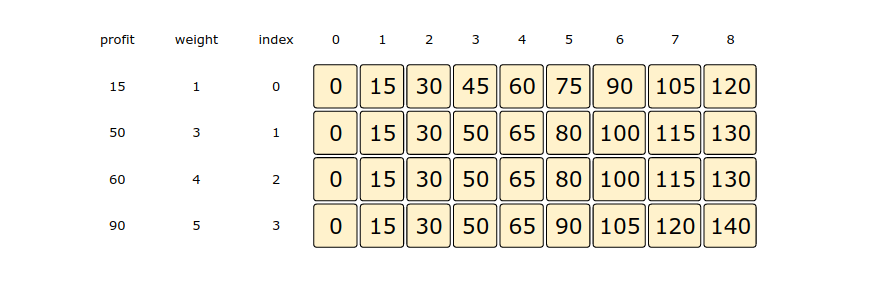
Here is the code for our bottom-up dynamic programming approach:
def solve_knapsack(profits, weights, capacity):
n = len(profits)
# base checks
if capacity <= 0 or n == 0 or len(weights) != n:
return 0
dp = [[-1 for _ in range(capacity+1)] for _ in range(len(profits))]
# populate the capacity=0 columns
for i in range(n):
dp[i][0] = 0
# process all sub-arrays for all capacities
for i in range(n):
for c in range(1, capacity+1):
profit1, profit2 = 0, 0
if weights[i] <= c:
profit1 = profits[i] + dp[i][c - weights[i]]
if i > 0:
profit2 = dp[i - 1][c]
dp[i][c] = profit1 if profit1 > profit2 else profit2
# maximum profit will be in the bottom-right corner.
return dp[n - 1][capacity]
def main():
print(solve_knapsack([15, 50, 60, 90], [1, 3, 4, 5], 8))
print(solve_knapsack([15, 50, 60, 90], [1, 3, 4, 5], 6))
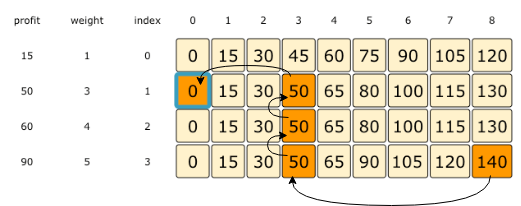
main()As we know, the final profit is at the right-bottom corner; hence we will start from there to find the items that will be going to the knapsack.
As you remember, at every step we had two options: include an item or skip it. If we skip an item, then we take the profit from the cell right above it; if we include the item, then we jump to the remaining profit to find more items.
Let’s assume the four items are identified as {A, B, C, and D}, and use the above example to better understand this:
140 did not come from the top cell (which is 130); hence we must include the item at index 3, which is D.
Subtract the profit of D from 140 to get the remaining profit 50. We then jump to profit 50 on the same row.
50 came from the top cell, so we jump to row 2.
Again, 50 came from the top cell, so we jump to row 1.
50 is different than the top cell, so we must include this item, which is B.
Subtract the profit of B from 50 to get the remaining profit 0. We then jump to profit 0 on the same row. As soon as we hit zero remaining profit, we can finish our item search.
So items going into the knapsack are {B, D}.
✓→ Rod Cutting