Longest Increasing Subsequence

Problem Statement

• Example 1

Input: {4,1,2,6,10,1,12}
Output: 32
Explanation: The increaseing sequence is {4,6,10,12}. 
Please note the difference, as the LIS is {1,2,6,10,12} which has a sum of '31'.

• Example 2

Input: {-4,10,3,7,15}
Output: 25
Explanation: The increaseing sequences are {10, 15} and {3,7,15}.

Basic Solution

The problem is quite similar to the Longest Increasing Subsequence. The only difference is that, instead of finding the increasing subsequence with the maximum length, we need to find an increasing sequence with the maximum sum.

A basic brute-force solution could be to try all the subsequences of the given array. We can process one number at a time, so we have two options at any step:

• If the current number is greater than the previous number that we included, we include that number in a running sum and make a recursive call for the remaining array.

• We can skip the current number to make a recursive call for the remaining array.

The highest sum of any increasing subsequence would be the max value returned by the two recurse calls from the above two options.

Code

Here is the code:

def find_MSIS(nums):
    return find_MSIS_recursive(nums, 0, -1, 0)


def find_MSIS_recursive(nums,  currentIndex,  previousIndex,  sum):
    if currentIndex == len(nums):
        return sum

    # include nums[currentIndex] if it is larger than the last included number
    s1 = sum
    if previousIndex == -1 or nums[currentIndex] > nums[previousIndex]:
        s1 = find_MSIS_recursive(nums, currentIndex+1,
                                 currentIndex, sum + nums[currentIndex])

    # excluding the number at currentIndex
    s2 = find_MSIS_recursive(nums, currentIndex+1, previousIndex, sum)

    return max(s1, s2)


def main():
    print(find_MSIS([4, 1, 2, 6, 10, 1, 12]))
    print(find_MSIS([-4, 10, 3, 7, 15]))


main()

Top-down Dynamic Programming with Memoization

We can use memoization to overcome the overlapping subproblems.

The three changing values for our recursive function are the current index, the previous index, and the sum. An efficient way of storing the results of the subproblems could be a hash-table whose key would be a string (currentIndex + “|” + previousIndex + “|” + sum).

Code

Here is the code:

def find_MSIS(nums):
    dp = {}
    return find_MSIS_recursive(dp, nums, 0, -1, 0)


def find_MSIS_recursive(dp, nums, currentIndex,  previousIndex,  sum):
    if currentIndex == len(nums):
        return sum

    subProblemKey = str(currentIndex) + "-" + \
        str(previousIndex) + "-" + str(sum)

    if subProblemKey not in dp:
        # include nums[currentIndex] if it is larger than the last included number
        s1 = sum
        if previousIndex == -1 or nums[currentIndex] > nums[previousIndex]:
            s1 = find_MSIS_recursive(
                dp, nums, currentIndex + 1, currentIndex, sum + nums[currentIndex])

        # excluding the number at currentIndex
        s2 = find_MSIS_recursive(
            dp, nums, currentIndex + 1, previousIndex, sum)
        dp[subProblemKey] = max(s1, s2)

    return dp.get(subProblemKey)


def main():
    print(find_MSIS([4, 1, 2, 6, 10, 1, 12]))
    print(find_MSIS([-4, 10, 3, 7, 15]))


main()

Bottom-up Dynamic Programming

The above algorithm tells us two things:

• If the number at the current index is bigger than the number at the previous index, we include that number in the sum for an increasing sequence up to the current index.

• But if there is a maximum sum increasing subsequence (MSIS), without including the number at the current index, we take that.

So we need to find all the increasing subsequences for a number at index i, from all the previous numbers (i.e. numbers till index i-1), to find MSIS.

If i represents the currentIndex and j represents the previousIndex, our recursive formula would look like:

if num[i] > num[j] => dp[i] = dp[j] + num[i] if there is no bigger MSIS for 'i'

Let’s draw this visually for {-4,10,3,7,15}. Start with a subsequence of length 1, as every number can represent an MSIS:

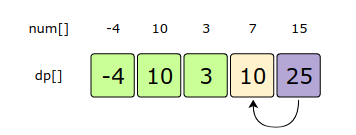
From the above visualization, we can clearly see that the maximum sum of any increasing subsequence is 25 – as shown by dp[4].

Code

Here is the code for our bottom-up dynamic programming approach:

def find_MSIS(nums):
    n = len(nums)
    dp = [0 for _ in range(n)]
    dp[0] = nums[0]

    maxSum = nums[0]
    for i in range(1, n):
        dp[i] = nums[i]
        for j in range(i):
            if nums[i] > nums[j] and dp[i] < dp[j] + nums[i]:
                dp[i] = dp[j] + nums[i]

        maxSum = max(maxSum, dp[i])

    return maxSum


def main():
    print(find_MSIS([4, 1, 2, 6, 10, 1, 12]))
    print(find_MSIS([-4, 10, 3, 7, 15]))


main()

Next