Shortest Common Super-sequence

Problem Statement

• Example 1

Input: s1: "abcf" s2:"bdcf" 
Output: 5
Explanation: The shortest common super-sequence (SCS) is "abdcf".

• Example 2

Input: s1: "dynamic" s2:"programming" 
Output: 15
Explanation: The SCS is "dynprogrammicng".

Basic Solution

The problem is quite similar to the Longest Common Subsequence.

A basic brute-force solution could be to try all the super-sequences of the given sequences. We can process both of the sequences one character at a time, so at any step, we must choose between:

• If the sequences have a matching character, we can skip one character from both the sequences and make a recursive call for the remaining lengths to get SCS.

• If the strings don’t match, we start two new recursive calls by skipping one character separately from each string. The minimum of these two recursive calls will have our answer.

Here is the code:

Code

Here is the code:

def find_SCS_length(s1, s2):
    return find_SCS_length_recursive(s1, s2, 0, 0)


def find_SCS_length_recursive(s1,  s2,  i1,  i2):
    # if we have reached the end of a string, return the remaining length of the
    # other string, as in this case we have to take all of the remaining other string
    n1, n2 = len(s1), len(s2)
    if i1 == n1:
        return n2 - i2
    if i2 == n2:
        return n1 - i1

    if s1[i1] == s2[i2]:
        return 1 + find_SCS_length_recursive(s1, s2, i1 + 1, i2 + 1)

    length1 = 1 + find_SCS_length_recursive(s1, s2, i1, i2 + 1)
    length2 = 1 + find_SCS_length_recursive(s1, s2, i1 + 1, i2)

    return min(length1, length2)


def main():
    print(find_SCS_length("abcf", "bdcf"))
    print(find_SCS_length("dynamic", "programming"))


main()

Top-down Dynamic Programming with Memoization

Let’s use memoization to overcome the overlapping subproblems.

The two changing values to our recursive function are the two indexes, i1 and i2. Therefore, we can store the results of all the subproblems in a two-dimensional array. (Another alternative could be to use a hash-table whose key would be a string (i1 + “|” + i2)).

Code

Here is the code:

def find_SCS_length(s1, s2):
    dp = {}
    return find_SCS_length_recursive(dp, s1, s2, 0, 0)


def find_SCS_length_recursive(dp, s1, s2,  i1,  i2):
    n1, n2 = len(s1), len(s2)
    # if we have reached the end of a string, return the remaining length of the
    # other string, as in this case we have to take all of the remaining other string
    if i1 == n1:
        return n2 - i2
    if i2 == n2:
        return n1 - i1
    subProblemKey = str(i1) + '-' + str(i2)
    if subProblemKey not in dp:
        if s1[i1] == s2[i2]:
            dp[subProblemKey] = 1 + \
                find_SCS_length_recursive(dp, s1, s2, i1 + 1, i2 + 1)
        else:
            length1 = 1 + find_SCS_length_recursive(dp, s1, s2, i1, i2 + 1)
            length2 = 1 + find_SCS_length_recursive(dp, s1, s2, i1 + 1, i2)
            dp[subProblemKey] = min(length1, length2)

    return dp[subProblemKey]


def main():
    print(find_SCS_length("abcf", "bdcf"))
    print(find_SCS_length("dynamic", "programming"))


main()

Bottom-up Dynamic Programming

Since we want to match all the subsequences of the given sequences, we can use a two-dimensional array to store our results. The lengths of the two strings will define the size of the array’s dimensions. So for every index i in sequence s1 and j in sequence s2, we will choose one of the following two options:

• If the character s1[i] matches s2[j], the length of the SCS would be the one plus the length of the SCS till i-1 and j-1 indexes in the two strings.

• If the character s1[i] does not match s2[j], we will consider two SCS: one without s1[i] and one without s2[j]. Our required SCS length will be the shortest of these two super-sequences plus one.

So our recursive formula would be:

if s1[i] == s2[j] 
    dp[i][j] = 1 + dp[i-1][j-1]
else 
    dp[i][j] = 1 + min(dp[i-1][j], dp[i][j-1])

Let’s draw this visually for “abcf” and “bdcf”. Starting with a subsequence of zero length. As we can see, if any strings have zero length, then the shortest super-sequence would be equal to the length of the other string:

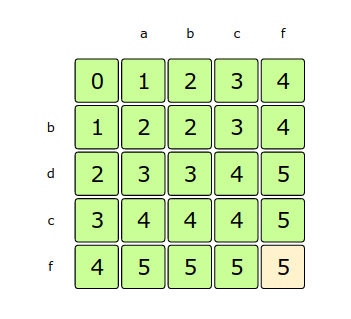
From the above visualization, we can clearly see that the longest increasing subsequence is of length 5 – as shown by dp[4][4].

Code

Here is the code for our bottom-up dynamic programming approach:

def find_SCS_length(s1, s2):
    n1, n2 = len(s1), len(s2)
    dp = [[0 for _ in range(len(s2)+1)] for _ in range(len(s1)+1)]

    # if one of the strings is of zero length, SCS would be equal to the length of the other string
    for i in range(n1+1):
        dp[i][0] = i
    for j in range(n2+1):
        dp[0][j] = j

    for i in range(1, n1+1):
        for j in range(1, n2+1):
            if s1[i-1] == s2[j-1]:
                dp[i][j] = 1 + dp[i-1][j-1]
            else:
                dp[i][j] = 1 + min(dp[i-1][j], dp[i][j-1])

    return dp[n1][n2]


def main():
    print(find_SCS_length("abcf", "bdcf"))
    print(find_SCS_length("dynamic", "programming"))


main()

Next