Palindromic Partitioning

Problem Statement

• Example 1

Input: "abdbca"
Output: 3
Explanation: Palindrome pieces are "a", "bdb", "c", "a".

• Example 2

Input: = "cddpd"
Output: 2
Explanation: Palindrome pieces are "c", "d", "dpd".

• Example 3

Input: = "pqr"
Output: 2
Explanation: Palindrome pieces are "p", "q", "r".

• Example 4

Input: = "pp"
Output: 0
Explanation: We do not need to cut, as "pp" is a palindrome.

Basic Solution

This problem follows the Longest Palindromic Subsequence pattern and shares a similar approach as that of the Longest Palindromic Substring.

The brute-force solution will be to try all the substring combinations of the given string. We can start processing from the beginning of the string and keep adding one character at a time. At any step, if we get a palindrome, we take it as one piece and recursively process the remaining length of the string to find the minimum cuts needed.

Code

Here is the code:

def find_MPP_cuts(st):
    return find_MPP_cuts_recursive(st, 0, len(st)-1)


def find_MPP_cuts_recursive(st, startIndex, endIndex):
    # we don't need to cut the string if it is a palindrome
    if startIndex >= endIndex or is_palindrome(st, startIndex, endIndex):
        return 0

    # at max, we need to cut the string into its 'length-1' pieces
    minimumCuts = endIndex - startIndex
    for i in range(startIndex, endIndex+1):
        if is_palindrome(st, startIndex, i):
            # we can cut here as we have a palindrome from 'startIndex' to 'i'
            minimumCuts = min(
                minimumCuts, 1 + find_MPP_cuts_recursive(st, i + 1, endIndex))

    return minimumCuts


def is_palindrome(st, x, y):
    while (x < y):
        if st[x] != st[y]:
            return False
        x += 1
        y -= 1
    return True


def main():
    print(find_MPP_cuts("abdbca"))
    print(find_MPP_cuts("cdpdd"))
    print(find_MPP_cuts("pqr"))
    print(find_MPP_cuts("pp"))
    print(find_MPP_cuts("madam"))


main()

Top-down Dynamic Programming with Memoization

We can memoize both functions findMPPCutsRecursive() and isPalindrome(). The two changing values in both these functions are the two indexes; therefore, we can store the results of all the subproblems in a two-dimensional array. (alternatively, we can use a hash-table).

Here is the code:

def find_MPP_cuts(st):
    n = len(st)
    dp = [[-1 for _ in range(n)] for _ in range(n)]
    dpIsPalindrome = [[-1 for _ in range(n)] for _ in range(n)]
    return find_MPP_cuts_recursive(dp, dpIsPalindrome, st, 0, n - 1)


def find_MPP_cuts_recursive(dp, dpIsPalindrome, st, startIndex, endIndex):

    if startIndex >= endIndex or is_palindrome(dpIsPalindrome, st, startIndex, endIndex):
        return 0

    if dp[startIndex][endIndex] == -1:
        # at max, we need to cut the string into its 'length-1' pieces
        minimumCuts = endIndex - startIndex
        for i in range(startIndex, endIndex+1):
            if is_palindrome(dpIsPalindrome, st, startIndex, i):
                # we can cut here as we have a palindrome from 'startIndex' to 'i'
                minimumCuts = min(
                    minimumCuts, 1 + find_MPP_cuts_recursive(dp, dpIsPalindrome, st, i + 1, endIndex))

        dp[startIndex][endIndex] = minimumCuts

    return dp[startIndex][endIndex]


def is_palindrome(dpIsPalindrome, st, x, y):
    if dpIsPalindrome[x][y] == -1:
        dpIsPalindrome[x][y] = 1
        i, j = x, y
        while i < j:
            if st[i] != st[j]:
                dpIsPalindrome[x][y] = 0
                break
            i += 1
            j -= 1
            # use memoization to find if the remaining string is a palindrome
            if i < j and dpIsPalindrome[i][j] != -1:
                dpIsPalindrome[x][y] = dpIsPalindrome[i][j]
                break

    return True if dpIsPalindrome[x][y] == 1 else False


def main():
    print(find_MPP_cuts("abdbca"))
    print(find_MPP_cuts("cdpdd"))
    print(find_MPP_cuts("pqr"))
    print(find_MPP_cuts("pp"))
    print(find_MPP_cuts("madam"))


main()

Bottom-up Dynamic Programming

The above solution tells us that we need to build two tables, one for the isPalindrome() and one for finding the minimum cuts needed.

If you remember, we built a table in the Longest Palindromic Substring (LPS) chapter that can tell us what substrings (of the input string) are palindrome. We will use the same approach here to build the table required for isPalindrome(). For example, here is the final output from LPS for “cddpd”. From this table we can clearly see that the substring(2,4) => 'dpd' is a palindrome:

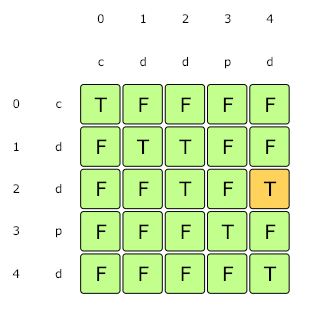
To build the second table for finding the minimum cuts, we can iterate through the first table built for isPalindrome(). At any step, if we get a palindrome, we can cut the string there. Which means minimum cuts will be one plus the cuts needed for the remaining string.

Here is the code for the bottom-up approach:

def find_MPP_cuts(st):
    n = len(st)
    # isPalindrome[i][j] will be 'true' if the string from index 'i' to index 'j' is a palindrome
    isPalindrome = [[False for _ in range(n)] for _ in range(n)]

    # every string with one character is a palindrome
    for i in range(n):
        isPalindrome[i][i] = True

    # populate isPalindrome table
    for startIndex in range(n-1, -1, -1):
        for endIndex in range(startIndex+1, n):
            if st[startIndex] == st[endIndex]:
                # if it's a two character string or if the remaining string is a palindrome too
                if endIndex - startIndex == 1 or isPalindrome[startIndex + 1][endIndex - 1]:
                    isPalindrome[startIndex][endIndex] = True

    # now lets populate the second table, every index in 'cuts' stores the minimum cuts needed
    # for the substring from that index till the end
    cuts = [0 for _ in range(n)]
    for startIndex in range(n-1, -1, -1):
        minCuts = n  # maximum cuts
        for endIndex in range(n-1, startIndex-1, -1):
            if isPalindrome[startIndex][endIndex]:
                # we can cut here as we got a palindrome
                # also we don't need any cut if the whole substring is a palindrome
                minCuts = 0 if endIndex == n - \
                    1 else min(minCuts, 1 + cuts[endIndex + 1])

        cuts[startIndex] = minCuts

    return cuts[0]


def main():
    print(find_MPP_cuts("abdbca"))
    print(find_MPP_cuts("cdpdd"))
    print(find_MPP_cuts("pqr"))
    print(find_MPP_cuts("pp"))
    print(find_MPP_cuts("madam"))


main()

Next