Longest Palindromic Substring

Problem Statement

• Example 1

Input: "abdbca"
Output: 3
Explanation: LPS is "bdb".

• Example 2

Input: = "cddpd"
Output: 3
Explanation: LPS is "dpd".

• Example 3

Input: = "pqr"
Output: 1
Explanation: LPS could be "p", "q" or "r".

Basic Solution

This problem follows the Longest Palindromic Subsequence pattern. The only difference is that in a palindromic subsequence characters can be non-adjacent, whereas in a substring all characters should form a palindrome. We will follow a similar approach though.

The brute-force solution will be to try all the substrings of the given string. We can start processing from the beginning and the end of the string. So at any step, we will have two options::

• If the element at the beginning and the end are the same, we make a recursive call to check if the remaining substring is also a palindrome. If so, the substring is a palindrome from beginning to the end.

• We will skip either the element from the beginning or the end to make two recursive calls for the remaining substring. The length of LPS would be the maximum of these two recursive calls.

Code

Here is the code:

def find_LPS_length(st):
    return find_LPS_length_recursive(st, 0, len(st) - 1)


def find_LPS_length_recursive(st, startIndex, endIndex):
    if startIndex > endIndex:
        return 0

    # every string with one character is a palindrome
    if startIndex == endIndex:
        return 1

    # case 1: elements at the beginning and the end are the same
    if st[startIndex] == st[endIndex]:
        remainingLength = endIndex - startIndex - 1
        # check if the remaining string is also a palindrome
        if remainingLength == find_LPS_length_recursive(st, startIndex + 1, endIndex - 1):
            return remainingLength + 2

    # case 2: skip one character either from the beginning or the end
    c1 = find_LPS_length_recursive(st, startIndex + 1, endIndex)
    c2 = find_LPS_length_recursive(st, startIndex, endIndex - 1)
    return max(c1, c2)


def main():
    print(find_LPS_length("abdbca"))
    print(find_LPS_length("cddpd"))
    print(find_LPS_length("pqr"))


main()

Top-down Dynamic Programming with Memoization

We can use an array to store the already solved subproblems.

The two changing values to our recursive function are the two indexes, startIndex and endIndex. Therefore, we can store the results of all the subproblems in a two-dimensional array. (Another alternative could be to use a hash-table whose key would be a string (startIndex + “|” + endIndex))

Code

Here is the code for this:

def find_LPS_length(st):
    n = len(st)
    dp = [[-1 for _ in range(n)] for _ in range(n)]
    return find_LPS_length_recursive(dp, st, 0, n - 1)


def find_LPS_length_recursive(dp, st, startIndex, endIndex):
    if startIndex > endIndex:
        return 0

    # every string with one character is a palindrome
    if startIndex == endIndex:
        return 1

    if dp[startIndex][endIndex] == -1:
        # case 1: elements at the beginning and the end are the same
        if st[startIndex] == st[endIndex]:
            remainingLength = endIndex - startIndex - 1
            # if the remaining string is a palindrome too
            if remainingLength == find_LPS_length_recursive(dp, st, startIndex + 1, endIndex - 1):
                dp[startIndex][endIndex] = remainingLength + 2
                return dp[startIndex][endIndex]

        # case 2: skip one character either from the beginning or the end
        c1 = find_LPS_length_recursive(dp, st, startIndex + 1, endIndex)
        c2 = find_LPS_length_recursive(dp, st, startIndex, endIndex - 1)
        dp[startIndex][endIndex] = max(c1, c2)

    return dp[startIndex][endIndex]


def main():
    print(find_LPS_length("abdbca"))
    print(find_LPS_length("cddpd"))
    print(find_LPS_length("pqr"))


main()

Bottom-up Dynamic Programming

Since we want to try all the substrings of the given string, we can use a two-dimensional array to store the subproblems’ results. So dp[i][j] will be true if the substring from index i to index j is a palindrome.

We can start from the beginning of the string and keep adding one element at a time. At every step, we will try all of its substrings. So for every endIndex and startIndex in the given string, we need to check the following thing:

If the element at the startIndex matches the element at the endIndex, we will further check if the remaining substring (from startIndex+1 to endIndex-1) is a substring too.

So our recursive formula will look like:

if st[startIndex] == st[endIndex], and 
        if the remaing string is of zero length or dp[startIndex+1][endIndex-1] is a palindrome then
   dp[startIndex][endIndex] = true

Let’s draw this visually for “cddpd”, starting with a substring of length 1. As we know, every substring with one element is a palindrome:

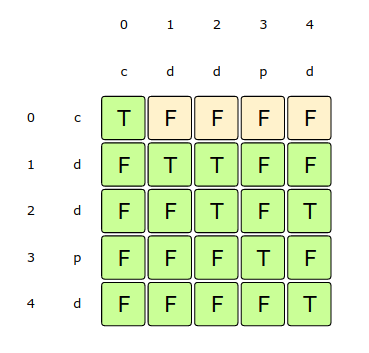
Here is the code for our bottom-up dynamic programming approach:

def find_LPS_length(st):
    n = len(st)
    # dp[i][j] will be 'true' if the string from index 'i' to index 'j' is a palindrome
    dp = [[False for _ in range(n)] for _ in range(n)]

    # every string with one character is a palindrome
    for i in range(n):
        dp[i][i] = True

    maxLength = 1
    for startIndex in range(n - 1, -1, -1):
        for endIndex in range(startIndex + 1, n):
            if st[startIndex] == st[endIndex]:
                # if it's a two character string or if the remaining string is a palindrome too
                if endIndex - startIndex == 1 or dp[startIndex + 1][endIndex - 1]:
                    dp[startIndex][endIndex] = True
                    maxLength = max(maxLength, endIndex - startIndex + 1)

    return maxLength


def main():
    print(find_LPS_length("abdbca"))
    print(find_LPS_length("cddpd"))
    print(find_LPS_length("pqr"))


main()

Manacher’s Algorithm

Next