Strings Interleaving

Problem Statement

• Example 1

Input: m="abd", n="cef", p="adcbef"
Output: false
Explanation: 'p' contains all the letters from 'm' and 'n' but does not preserve the order.

• Example 2

Input: m="abc", n="def", p="abdccf"
Output: false
Explanation: 'p' does not contain all the letters from 'm' and 'n'.

• Example 3

Input: m="abcdef", n="mnop", p="mnaobcdepf"
Output: true
Explanation: 'p' contains all the letters from 'm' and 'n' and preserves their order too.

Basic Solution

The problem follows the Longest Common Subsequence (LCS) pattern and has some similarities with Subsequence Pattern Matching.

A basic brute-force solution could be to try matching m and n with p one letter at a time. Let’ s assume mIndex, nIndex, and pIndex represent the current indexes of m, n, and p strings respectively. Therefore, we have two options at any step:

If the letter at mIndex matches with the letter at pIndex, we can recursively match for the remaining lengths of m and p. If the letter at nIndex matches with the letter at ‘pIndex’, we can recursively match for the remaining lengths of n and p.

Code

Here is the code:

def find_SI(m, n,  p):
    return find_SI_recursive(m, n, p, 0, 0, 0)


def find_SI_recursive(m, n, p, mIndex, nIndex, pIndex):

    mLen, nLen, pLen = len(m), len(n), len(p)
    # if we have reached the end of the all the strings
    if mIndex == mLen and nIndex == nLen and pIndex == pLen:
        return True

    # if we have reached the end of 'p' but 'm' or 'n' still has some characters left
    if pIndex == pLen:
        return False

    b1, b2 = False, False
    if mIndex < mLen and m[mIndex] == p[pIndex]:
        b1 = find_SI_recursive(m, n, p, mIndex+1, nIndex, pIndex+1)

    if nIndex < nLen and n[nIndex] == p[pIndex]:
        b2 = find_SI_recursive(m, n, p, mIndex, nIndex+1, pIndex+1)

    return b1 or b2


def main():
    print(find_SI("abd", "cef", "abcdef"))
    print(find_SI("abd", "cef", "adcbef"))
    print(find_SI("abc", "def", "abdccf"))
    print(find_SI("abcdef", "mnop", "mnaobcdepf"))


main()

Top-down Dynamic Programming with Memoization

This problem can have overlapping subproblems only when there are some common letters between m and n at the same index. Because whenever we hit such a scenario, we get an option to match with any one of them.

The three changing values in our recursive function are the three indexes mIndex, nIndex, and pIndex. Therefore, we can store the results of all the subproblems in a three-dimensional array. Alternately, we can use a hash-table whose key would be a string (mIndex + “|” + nIndex + “|” + pIndex).

Code

Here is the code for Top-down DP approach:

def find_SI(m, n, p):
    return find_SI_recursive({}, m, n, p, 0, 0, 0)


def find_SI_recursive(dp, m, n, p, mIndex, nIndex, pIndex):
    mLen, nLen, pLen = len(m), len(n), len(p)
    # if we have reached the end of the all the strings

    if mIndex == mLen and nIndex == nLen and pIndex == pLen:
        return True

    # if we have reached the end of 'p' but 'm' or 'n' still has some characters left
    if pIndex == pLen:
        return False

    subProblemKey = str(mIndex) + "-" + str(nIndex) + "-" + str(pIndex)
    if subProblemKey not in dp:
        b1, b2 = False, False
        if mIndex < mLen and m[mIndex] == p[pIndex]:
            b1 = find_SI_recursive(dp, m, n, p, mIndex + 1, nIndex, pIndex + 1)

        if nIndex < nLen and n[nIndex] == p[pIndex]:
            b2 = find_SI_recursive(dp, m, n, p, mIndex, nIndex + 1, pIndex + 1)

        dp[subProblemKey] = b1 or b2

    return dp.get(subProblemKey)


def main():
    print(find_SI("abd", "cef", "abcdef"))
    print(find_SI("abd", "cef", "adcbef"))
    print(find_SI("abc", "def", "abdccf"))
    print(find_SI("abcdef", "mnop", "mnaobcdepf"))


main()

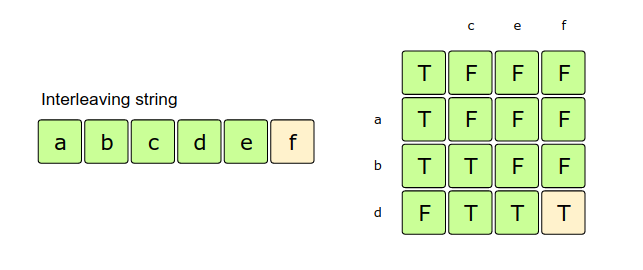
Bottom-up Dynamic Programming

Since we want to completely match m and n (the two interleaving strings) with p, we can use a two-dimensional array to store our results. The lengths of m and n will define the dimensions of the result array.

As mentioned above, we will be tracking separate indexes for m, n and p, so we will have the following options for every value of mIndex, nIndex, and pIndex:

• If the character m[mIndex] matches the character p[pIndex], we will take the matching result up to mIndex-1 and nIndex.

• If the character n[nIndex] matches the character p[pIndex], we will take the matching result up to mIndex and nIndex-1.

String p will be interleaving strings m and n if any of the above two options is true. This is also required as there could be some common letters between m and n.

So our recursive formula would look like:

dp[mIndex][nIndex] = false
if m[mIndex] == p[pIndex] 
    dp[mIndex][nIndex] = dp[mIndex-1][nIndex]
if n[nIndex] == p[pIndex] 
    dp[mIndex][nIndex] |= dp[mIndex][nIndex-1]

Let’s draw this visually:

Code

Here is the code for our bottom-up dynamic programming approach:

def find_SI(m, n, p):
    mLen, nLen, pLen = len(m), len(n), len(p)
    # dp[mIndex][nIndex] will be storing the result of string interleaving
    # up to p[0..mIndex+nIndex-1]
    dp = [[False for _ in range(nLen+1)] for _ in range(mLen+1)]

    # make sure if lengths of the strings add up
    if mLen + nLen != pLen:
        return False

    for mIndex in range(mLen+1):
        for nIndex in range(nLen+1):
            # if 'm' and 'n' are empty, then 'p' must have been empty too.
            if mIndex == 0 and nIndex == 0:
                dp[mIndex][nIndex] = True
            # if 'm' is empty, we need to check the interleaving with 'n' only
            elif mIndex == 0 and n[nIndex - 1] == p[mIndex + nIndex - 1]:
                dp[mIndex][nIndex] = dp[mIndex][nIndex - 1]
            # if 'n' is empty, we need to check the interleaving with 'm' only
            elif nIndex == 0 and m[mIndex - 1] == p[mIndex + nIndex - 1]:
                dp[mIndex][nIndex] = dp[mIndex - 1][nIndex]
            else:
                # if the letter of 'm' and 'p' match, we take whatever is matched till mIndex-1
                if mIndex > 0 and m[mIndex - 1] == p[mIndex + nIndex - 1]:
                    dp[mIndex][nIndex] = dp[mIndex - 1][nIndex]
                # if the letter of 'n' and 'p' match, we take whatever is matched till nIndex-1 too
                # note the '|=', this is required when we have common letters
                if nIndex > 0 and n[nIndex - 1] == p[mIndex + nIndex - 1]:
                    dp[mIndex][nIndex] |= dp[mIndex][nIndex - 1]

    return dp[mLen][nLen]


def main():
    print(find_SI("abd", "cef", "abcdef"))
    print(find_SI("abd", "cef", "adcbef"))
    print(find_SI("abc", "def", "abdccf"))
    print(find_SI("abcdef", "mnop", "mnaobcdepf"))


main()