Longest Alternating Subsequence

Problem Statement

{a1 > a2 < a3 } or { a1 < a2 > a3}.

• Example 1

Input: {1,2,3,4}
Output: 2
Explanation: There are many LAS: {1,2}, {3,4}, {1,3}, {1,4}

• Example 2

Input: {3,2,1,4}
Output: 3
Explanation: The LAS are {3,2,4} and {2,1,4}.

• Example 3

Input: {1,3,2,4}
Output: 4
Explanation: The LAS is {1,3,2,4}.

Basic Solution

A basic brute-force solution could be to try finding the LAS starting from every number in both ascending and descending order. So for every index i in the given array, we will have three options:

• If the element at i is bigger than the last element we considered, we include the element at i and recursively process the remaining array to find the next element in descending order.

• If the element at i is smaller than the last element we considered, we include the element at i and recursively process the remaining array to find the next element in ascending order.

• In addition to the above two cases, we can always skip the element i to recurse for the remaining array. This will ensure that we try all subsequences.

LAS would be the maximum of the above three subsequences.

Code

Here is the code:

def find_LAS_length(nums):
    # we have to start with two recursive calls, one where we will consider that the first element is
    # bigger than the second element and one where the first element is smaller than the second element
    return max(find_LAS_length_recursive(nums, -1, 0, True), find_LAS_length_recursive(nums, -1, 0, False))


def find_LAS_length_recursive(nums,  previousIndex,  currentIndex,  isAsc):
    if currentIndex == len(nums):
        return 0

    c1 = 0
    # if ascending, the next element should be bigger
    if isAsc:
        if previousIndex == -1 or nums[previousIndex] < nums[currentIndex]:
            c1 = 1 + \
                find_LAS_length_recursive(
                    nums, currentIndex, currentIndex + 1, not isAsc)
    else:  # if descending, the next element should be smaller
        if previousIndex == -1 or nums[previousIndex] > nums[currentIndex]:
            c1 = 1 + \
                find_LAS_length_recursive(
                    nums, currentIndex, currentIndex + 1, not isAsc)
    # skip the current element
    c2 = find_LAS_length_recursive(
        nums, previousIndex, currentIndex + 1, isAsc)
    return max(c1, c2)


def main():
    print(find_LAS_length([1, 2, 3, 4]))
    print(find_LAS_length([3, 2, 1, 4]))
    print(find_LAS_length([1, 3, 2, 4]))


main()

Top-down Dynamic Programming with Memoization

To overcome the overlapping subproblems, we can use an array to store the already solved subproblems.

The three changing values for our recursive function are the current and the previous indexes and the isAsc flag. Therefore, we can store the results of all subproblems in a three-dimensional array, where the third dimension will be of size two, to store the boolean flag isAsc. (Another alternative could be to use a hash-table whose key would be a string (currentIndex + “|” + previousIndex + “|” + isAsc)).

Code

Here is the code:

def find_LAS_length(nums):
    n = len(nums)
    dp = {}
    return max(find_LAS_length_recursive(dp, nums, -1, 0, True),
               find_LAS_length_recursive(dp, nums, -1, 0, False))


def find_LAS_length_recursive(dp, nums, previousIndex, currentIndex,  isAsc):

    if currentIndex == len(nums):
        return 0

    keyWord = str(previousIndex + 1) + '-' + \
        str(currentIndex) + '-' + str(1 if isAsc else 0)
    if keyWord not in dp:
        c1 = 0
        # if ascending, the next element should be bigger
        if isAsc:
            if previousIndex == -1 or nums[previousIndex] < nums[currentIndex]:
                c1 = 1 + \
                    find_LAS_length_recursive(
                        dp, nums, currentIndex, currentIndex + 1, not isAsc)
        else:  # if descending, the next element should be smaller
            if previousIndex == -1 or nums[previousIndex] > nums[currentIndex]:
                c1 = 1 + \
                    find_LAS_length_recursive(
                        dp, nums, currentIndex, currentIndex + 1, not isAsc)

        # skip the current element
        c2 = find_LAS_length_recursive(
            dp, nums, previousIndex, currentIndex + 1, isAsc)
        dp[keyWord] = max(c1, c2)

    return dp[keyWord]


def main():
    print(find_LAS_length([1, 2, 3, 4]))
    print(find_LAS_length([3, 2, 1, 4]))
    print(find_LAS_length([1, 3, 2, 4]))


main()

Bottom-up Dynamic Programming

The above algorithm tells us three things:

• We need to find an ascending and descending subsequence at every index.

• While finding the next element in the ascending order, if the number at the current index is bigger than the number at the previous index, we increment the count for a LAS up to the current index. But if there is a bigger LAS without including the number at the current index, we take that.

• Similarly for the descending order, if the number at the current index is smaller than the number at the previous index, we increment the count for a LAS up to the current index. But if there is a bigger LAS without including the number at the current index, we take that.

To find the largest LAS, we need to find all of the LAS for a number at index i from all the previous numbers (i.e. number till index i-1).

We can use two arrays to store the length of LAS, one for ascending order and one for descending order. (Actually, we will use a two-dimensional array, where the second dimension will be of size two).

If i represents the currentIndex and j represents the previousIndex, our recursive formula would look like:

• If nums[i] is bigger than nums[j] then we will consider the LAS ending at j where the last two elements were in descending order =>

if num[i] > num[j] => dp[i][0] = 1 + dp[j][1], if there is no bigger LAS for 'i'

• If nums[i] is smaller than nums[j] then we will consider the LAS ending at j where the last two elements were in ascending order =>

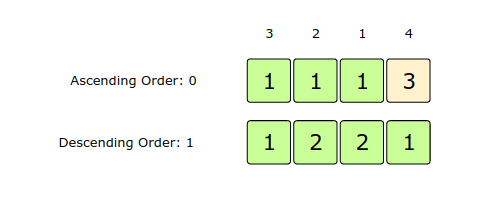
if num[i] < num[j] => dp[i][1] = 1 + dp[j][0], if there is no bigger LAS for 'i'

Let’ s draw this visually for {3,2,1,4}. Start with a subsequence of length 1, as every number can be a LAS of length 1:

Code

Here is the code for our bottom-up dynamic programming approach:

def find_LAS_length(nums):
    n = len(nums)
    if n == 0:
        return 0
    # dp[i][0] = stores the LAS ending at 'i' such that the last two elements are in ascending order
    # dp[i][1] = stores the LAS ending at 'i' such that the last two elements are in descending order
    dp = [[0 for _ in range(2)] for _ in range(n)]
    maxLength = 1
    for i in range(n):
        # every single element can be considered as LAS of length 1
        dp[i][0] = dp[i][1] = 1
        for j in range(i):
            if nums[i] > nums[j]:
                # if nums[i] is BIGGER than nums[j] then we will consider the LAS ending at 'j' where the
                # last two elements were in DESCENDING order
                dp[i][0] = max(dp[i][0], 1 + dp[j][1])
                maxLength = max(maxLength, dp[i][0])
            elif nums[i] != nums[j]:  # if the numbers are equal don't do anything
                # if nums[i] is SMALLER than nums[j] then we will consider the LAS ending at
                # 'j' where the last two elements were in ASCENDING order
                dp[i][1] = max(dp[i][1], 1 + dp[j][0])
                maxLength = max(maxLength, dp[i][1])
    return maxLength


def main():
    print(find_LAS_length([1, 2, 3, 4]))
    print(find_LAS_length([3, 2, 1, 4]))
    print(find_LAS_length([1, 3, 2, 4]))


main()

Next