CountWays(3), CountWays(2) and CountWays(1) have been called twice. We can optimize this using memoization to store the results for subproblems.n, implement a method to count how many possible ways there are to express n as the sum of 1, 3, or 4.Example1
n : 4
Number of ways = 4
Explanation: Following are the four ways we can express 'n' : {1,1,1,1}, {1,3}, {3,1}, {4}Example2
n : 5
Number of ways = 6
Explanation: Following are the six ways we can express 'n' : {1,1,1,1,1}, {1,1,3}, {1,3,1}, {3,1,1},
{1,4}, {4,1}Let’ s first start with a recursive brute-force solution.
For every number i, we have three option: subtract either 1, 3, or 4 from i and recursively process the remaining number. So our algorithm will look like:
def count_ways(n):
if n == 0:
return 1 # base case, we don't need to subtract any thing, so there is only one way
if n == 1:
return 1 # we take subtract 1 to be left with zero, and that is the only way
if n == 2:
return 1 # we can subtract 1 twice to get zero and that is the only way
if n == 3:
return 2 # '3' can be expressed as {1, 1, 1}, {3}
# if we subtract 1, we are left with 'n-1'
subtract1 = count_ways(n - 1)
# if we subtract 3, we are left with 'n-3'
subtract3 = count_ways(n - 3)
# if we subtract 4, we are left with 'n-4'
subtract4 = count_ways(n - 4)
return subtract1 + subtract3 + subtract4
def main():
print(count_ways(4))
print(count_ways(5))
print(count_ways(6))
main()Let’s visually draw the recursion for CountWays(5) to see the overlapping subproblems:
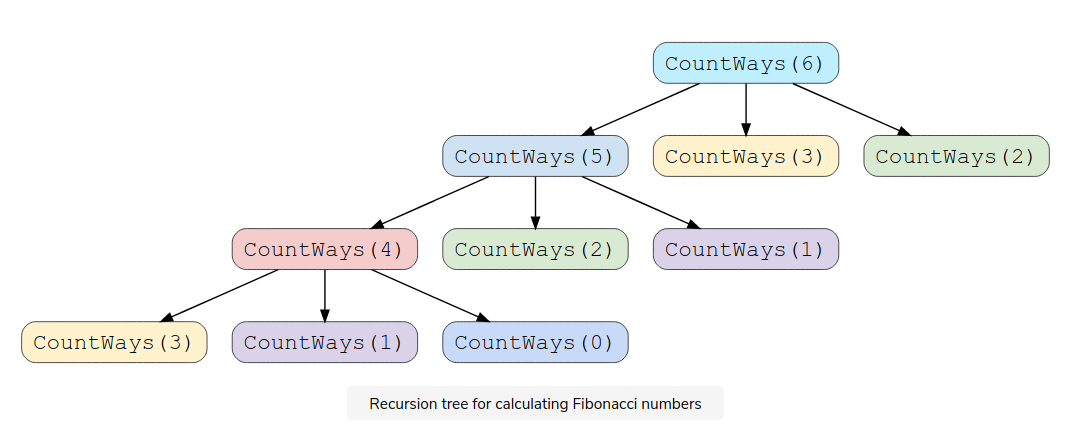
CountWays(3), CountWays(2) and CountWays(1) have been called twice. We can optimize this using memoization to store the results for subproblems.We can use an array to store the already solved subproblems. Here is the code:
def count_ways(n):
dp = [0 for x in range(n+1)]
return count_ways_recursive(dp, n)
def count_ways_recursive(dp, n):
if n == 0:
return 1 # base case, we don't need to subtract any thing, so there is only one way
if n == 1:
return 1 # we can take subtract 1 to be left with zero, and that is the only way
if n == 2:
return 1 # we can subtract 1 twice to get zero and that is the only way
if n == 3:
return 2 # '3' can be expressed as {1, 1, 1}, {3}
if dp[n] == 0:
# if we subtract 1, we are left with 'n-1'
subtract1 = count_ways_recursive(dp, n - 1)
# if we subtract 3, we are left with 'n-3'
subtract3 = count_ways_recursive(dp, n - 3)
# if we subtract 4, we are left with 'n-4'
subtract4 = count_ways_recursive(dp, n - 4)
dp[n] = subtract1 + subtract3 + subtract4
return dp[n]
def main():
print(count_ways(4))
print(count_ways(5))
print(count_ways(6))
main()Let’s try to populate our dp[] array from the above solution, working in a bottom-up fashion. As we saw in the above code, every CountWaysRecursive(n) is the sum of the three counts. We can use this fact to populate our array.
Here is the code for our bottom-up dynamic programming approach:
def count_ways(n):
if n <= 2:
return 1
if n == 3:
return 2
dp = [0 for x in range(n+1)]
dp[0] = 1
dp[1] = 1
dp[2] = 1
dp[3] = 2
for i in range(4, n+1):
dp[i] = dp[i - 1] + dp[i - 3] + dp[i - 4]
return dp[n]
def main():
print(count_ways(4))
print(count_ways(5))
print(count_ways(6))
main()We can clearly see that this problem follows the Fibonacci number pattern. However, every number in a Fibonacci series is the sum of the previous two numbers, whereas in this problem every count is a sum of previous three numbers: previous-1, previous-3, and previous-4. Here is the recursive formula for this problem:
CountWays(n) = CountWays(n-1) + CountWays(n-3) + CountWays(n-4), for n >= 4✓→ Minimum jumps to reach the end