0/1 Knapsack

Problem Statement

Mathematically we can define the Fibonacci numbers as:

Fib(n) = Fib(n-1) + Fib(n-2), for n > 1
Given that: Fib(0) = 0, and Fib(1) = 1

Basic Solution

A basic solution could be to have a recursive implementation of the mathematical formula discussed above:

def calculateFibonacci(n):
    if n < 2:
        return n

    return calculateFibonacci(n - 1) + calculateFibonacci(n - 2)


def main():
    print("5th Fibonacci is ---> " + str(calculateFibonacci(5)))
    print("6th Fibonacci is ---> " + str(calculateFibonacci(6)))
    print("7th Fibonacci is ---> " + str(calculateFibonacci(7)))


main()

Let’s visually draw the recursion for CalculateFibonacci(4) to see the overlapping subproblems:

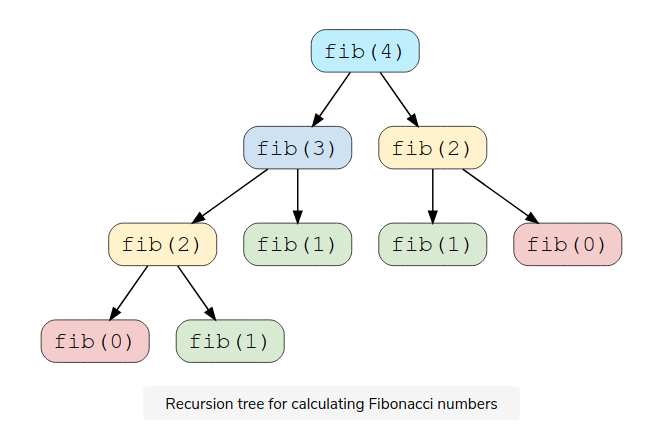
We can clearly see the overlapping subproblem pattern: fib(2) has been called twice and fib(1) has been called thrice. We can optimize this using memoization to store the results for subproblems.

Top-down Dynamic Programming with Memoization

We can use an array to store the already solved subproblems. Here is the code:

def calculateFibonacci(n):
    memoize = [-1 for x in range(n+1)]
    return calculateFibonacciRecur(memoize, n)


def calculateFibonacciRecur(memoize, n):
    if n < 2:
        return n

    # if we have already solved this subproblem, simply return the result from the cache
    if memoize[n] >= 0:
        return memoize[n]

    memoize[n] = calculateFibonacciRecur(
        memoize, n - 1) + calculateFibonacciRecur(memoize, n - 2)
    return memoize[n]


def main():
    print("5th Fibonacci is ---> " + str(calculateFibonacci(5)))
    print("6th Fibonacci is ---> " + str(calculateFibonacci(6)))
    print("7th Fibonacci is ---> " + str(calculateFibonacci(7)))


main()

Bottom-up Dynamic Programming

Let’s try to populate our dp[] array from the above solution, working in a bottom-up fashion. Since every Fibonacci number is the sum of the previous two numbers, we can use this fact to populate our array.

Here is the code for the bottom-up dynamic programming approach:

def calculateFibonacci(n):
    if n < 2:
        return n
    dp = [0, 1]
    for i in range(2, n + 1):
        dp.append(dp[i - 1] + dp[i - 2])

    return dp[n]


def main():
    print("5th Fibonacci is ---> " + str(calculateFibonacci(5)))
    print("6th Fibonacci is ---> " + str(calculateFibonacci(6)))
    print("7th Fibonacci is ---> " + str(calculateFibonacci(7)))


main()

Memory optimization

We can optimize the space used in our previous solution. We don’t need to store all the Fibonacci numbers up to n, as we only need two previous numbers to calculate the next Fibonacci number. We can use this fact to further improve our solution:

def calculateFibonacci(n):
    if n < 2:
        return n

    n1, n2, temp = 0, 1, 0
    for i in range(2, n + 1):
        temp = n1 + n2
        n1 = n2
        n2 = temp

    return n2


def main():
    print("5th Fibonacci is ---> " + str(calculateFibonacci(5)))
    print("6th Fibonacci is ---> " + str(calculateFibonacci(6)))
    print("7th Fibonacci is ---> " + str(calculateFibonacci(7)))


main()

Next